tensorflow-二十八弹
条评论上一次的学习过程中介绍了RNN,然后列举了它的流程以及理解,然后运行代码试了一下,有了一个直观的体会,但是代码的逻辑实际上还是比较奇怪,而且列出的公式也不直观,实际上在27弹中所提到了公式是进行简化了的公式,所以看起来会比较复杂一些,这次在深入理解之后重新梳理了一下,然后把公式串起来。
还是上面这张图,这张图其实描述得有点含糊,为了更清晰得说明情况我再加上一张图进行说明:

上图来自网络,侵删联系。把两张图结合起来看就比较好了,实际上对于一个序列输入$[x_1,x_2…x_n]$来说再训练得时候其实不必要关心每次得输入对应得输出,我们更关心的是最后的输入和输出结果。所以对于每一步实际上最重要的是中间层,从两个图中我们可以得到中间层的计算方法,为了统一我们公式表示都参考第一张图,其中$s_t$为中间层:
$$
s_t=f(Ws_{t-1}+Ux_t+b)(1)
$$
公式(1)中$s_t$为当前状态的隐含层,$W$为上一个隐含层到当前隐含层的权重,$U$为输入到隐含层的权重。这样我们就得到了从输入到隐含层的计算方式,然后我们从隐含层到输出:
$$
o_t=g(V*s_t+c)(2)
$$
在公式(2)中$o_t$为输出结果,$V$为输入到输出的权重,然后我们就得到了整个卷积神经网络的经典公式。对比上次给出的公式:
二十七弹中的公式为:
$$
\begin{aligned}
&S_t=f(W(Xt@ S{t-1})+b)(3)\
&O_t=g(US_t,+c)(4)
\end{aligned}
$$
从比较中可以看出实际上主要的差别集中在(1)和(3)上,实际上在二十七弹中给出的公式是简化公式,我们可以把式(1)写成如下形式:
$$
s_t=f([W,U]\cdot[s_{t-1},x_t]’+b))(5)
$$
对于式(5)其实就是将$W$与$U$合并为一个矩阵再将$s_{t-1},x_t$合并,其中$@$符号就是矩阵合并的符号,由于python矩阵合并计算相对比较简单因此采用简化公式能够减小编码量,但是却增大的理解的负担;实际上序列不可能无限长,因此每次都是截取一定长度的序列进行计算,由此产生了step参数。
实际上经典的RNN已经了解了,但是在应用过程中RNN存在很多变化比如以下几种图的变化:
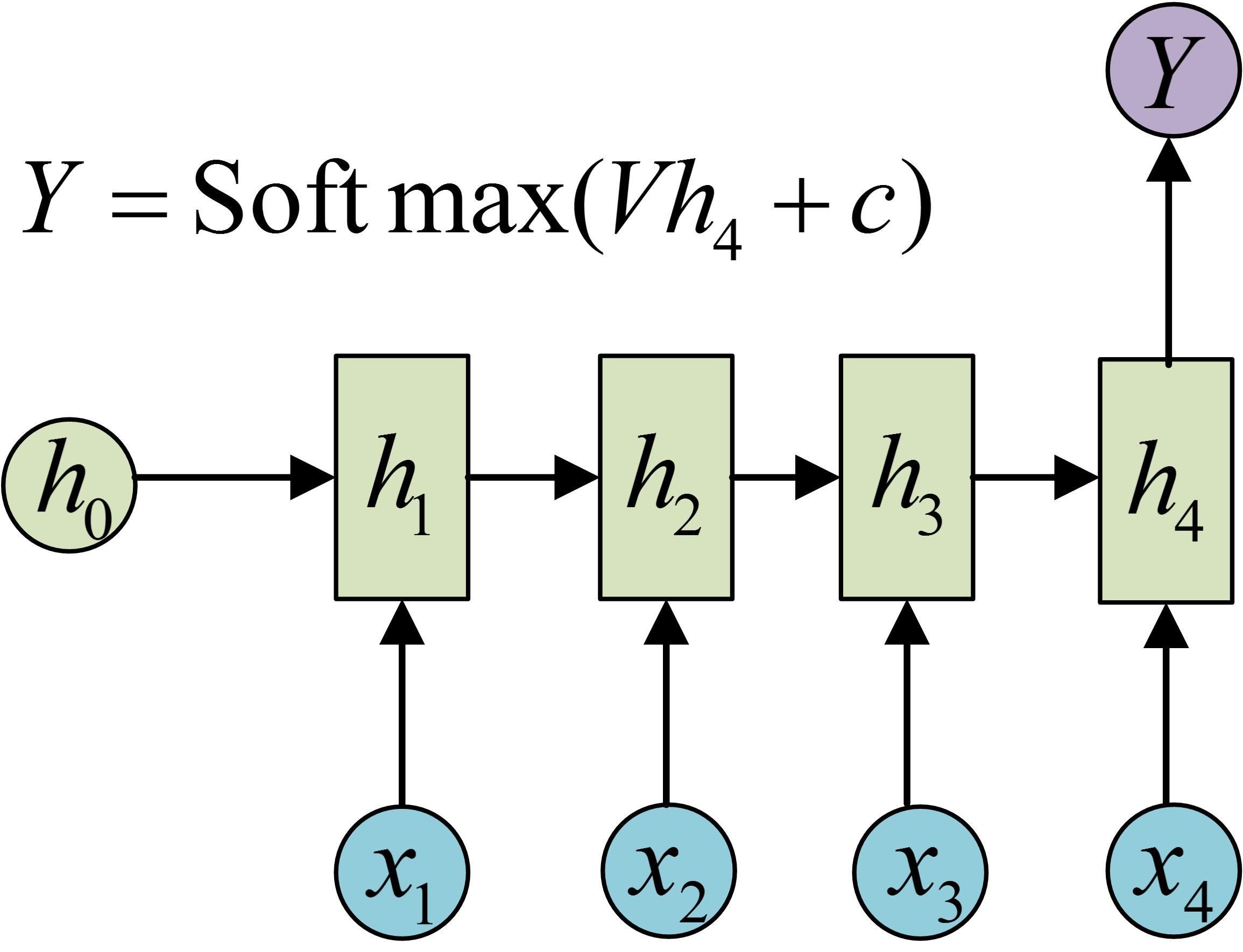
图1.多个输入对应一个输出
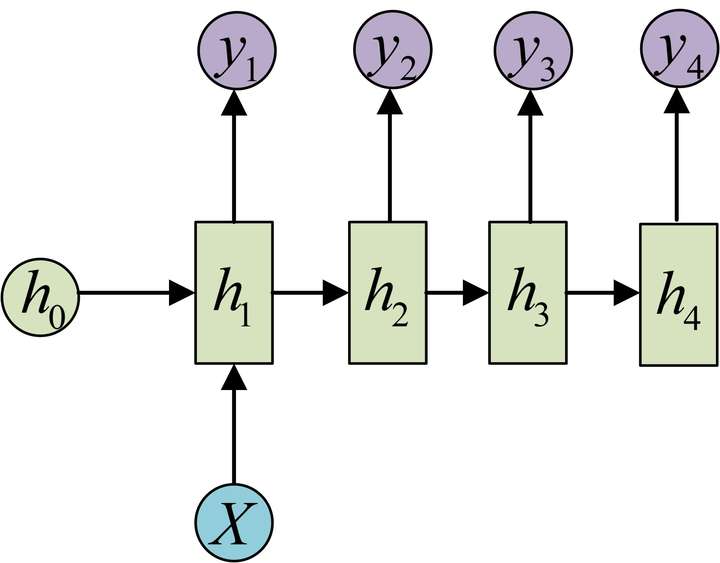
图2.一个输入对应多个输出
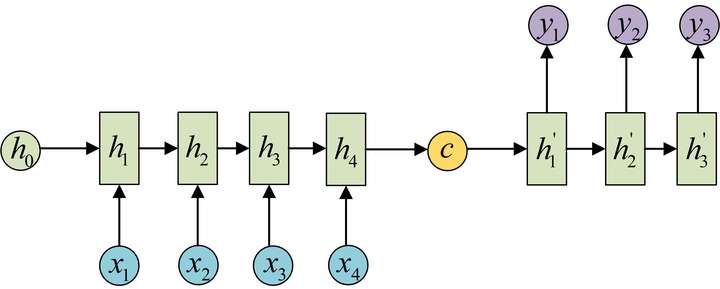
图3.自编码解码器
以上三种是RNN中除了输入与输出等长之外最常见的三种模式了,实际上前两种都比较简单,对于多个输入对应一个输出的模式,只需要在最后一个输出上对应进行变换就好了。而对于多个输出对应一个输入的只需要对最开始的输入进行变换。整个结构没有变化过程也比较简单,单独把最后或者第一次的输入或者输出抽取出来就好了;对于多个输入对应一个输出的情况一般都是在语义的识别中,比如输入一个语句判断其情感倾向等。一个输入对应多个输出情况就比较多,比如输入第一画自动绘制,输入描述自动生成文字图片等都属于这一类。第三类是最重要的一个部分,我们叫自编码器;实际上就是根据输入得到一个输入的编码对于不同的输入都能够得到统一的编码形式使得输入数据能够统一,另外编码也能够包含输入的所有信息。编码的形式有很多种,可以直接输出最后一个隐藏状态,也可以对最后一个隐藏状态进行变换或者对所有隐藏状态进行变换得到结果。得到这个结果我们就认为是对序列输入的编码结果,而过程中的参数实际上就是编码器。有编码过程就一定有一个解码过程,解码过程就是由c得到各个输出的过程。解码实际上也是一个RNN网络,这个网络的结构就是图2中提到的多个输入对应一个输出的结构。然后训练出一个网络。这样就得到了两个网络,这一组网络我们就称为编码-解码器。编码器的优点在于不对输入和输出的长度进行限制,因此被广泛的应用。参考内容
通过这次学习解决了上次遗留的一些问题,同时对RNN的结构进行了归纳,同时对编码器进行了理解,实际上通过这个结构对自编码器就能够很好的理解了。通过学习编码形式得到输出和其本身对接近的编码器和解码器从而实现对数据的抽象,对于小样本的学习来说通过自编码的形式能够对数据进行更高层次的抽象,在此基础上通过少量的样本可以达到很好的学习效果。