摄影测量P矩阵
条评论对于理解P矩阵,首先需要理解几个坐标系如图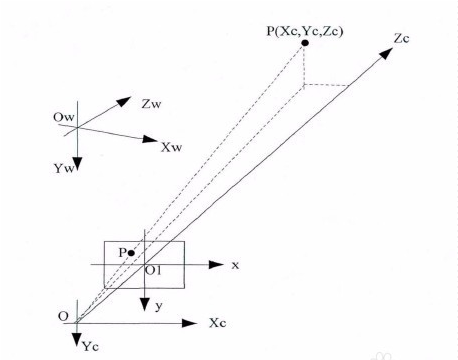
分别为像平面坐标系,像空间坐标系,物方坐标系以及世界坐标系。在讨论的过程中我们暂时不考虑世界坐标系,和像平面坐标系,只考虑像方和物方坐标系如图: 上图中C点为摄影机中心,也认为是坐标系原点,p点为图像中心,假设图像上任意(x,y,f)对应的物方坐标系中的点为(X,Y,Z),则根据三角形相似我们可以列出如下公式:
$$
\frac{x}{X}=\frac{y}{Y}=\frac{f}{Z}(1)
$$
实际上以上的(x,y,f)为像空间坐标系中的坐标,对于影像来说,我们获取的坐标为像素坐标,像素坐标是以图像的左上角点为原点沿着图像方向的坐标系统,这里有一个转换公式$x=u_x-x_0,y=y_0-u_y$其中$u_x,x_0,y_0,u_y$分别为x方向像素坐标,像主点的水平中心,y方向像素坐标,像主点垂直中;因此将像素坐标代入公式(1)可得:
$$
\frac{u_x-x_0}{X}=\frac{y_0-u_y}{Y}=\frac{f}{Z}(2)
$$
则根据式(2)可得:
$$
u_x = X\frac{f}{Z}+x_0->Zu_x=Xf+Zx_0(3)
$$
$$
u_y = -Y\frac{f}{Z}+y_0->Zu_y=-Yf+Zy_0(4)
$$
根据以上两式可得:$(Zu_x,Zu_y,Z)=(Xf+Zx_0,-Yf+Z-y_0,Z)$将其写成矩阵的形式则有
$$
Z(u_x,u_y,1)=
\begin{bmatrix}1&0&0\\ 0&-1&0\\ 0&0&1\end{bmatrix}\cdot
\begin{bmatrix}f&0&x_0\\ 0&f&y_0\\ 0&0&1\end{bmatrix}\cdot
\begin{bmatrix}X\\ Y\\ Z\end{bmatrix}(5)
$$
以上就式像平面坐标系到物方坐标系的转换,实际上以上矩阵分为三个部分,第一个部分是由于像素坐标和像平面坐标引起的,主要体现坐标轴的方向,第二个部分主要式内方位元素,也就是通常所说的内参,而第三个部分主要是像方坐标系的坐标,根据式(5)实际上可以建立起图像坐标到物方坐标的关系。然而在真实世界中坐标原点往往不是摄影中心,摄影中心和世界坐标系的原点往往存在着一个偏移,另外以影像坐标为原点的坐标系中x轴与y轴与像平面平行,而z轴垂直于像平面。对于真实世界坐标系,以摄影中心为原点的坐标系与世界坐标之间存在着角度的偏移,因此将物方坐标系校正到世界坐标系的过程中存在两个步骤:1.角度的校正;2.位置的平移,角度的校正通过旋转矩阵来实现,而位置的平移则通过平移向量实现,则在此过程中三个角度和三个平移向量就构成了我们通常说的外方位元素。则像方坐标系到世界坐标系的转换公式为:
$$
\begin{bmatrix}X_w\\ Y_w\\ Z_w\end{bmatrix}=
\begin{bmatrix}a_1&a_2&a_3\\ b_1&b_2&b_3\\ c_1&c_2&c_3\end{bmatrix}\cdot
\begin{bmatrix}X\\ Y\\ Z\end{bmatrix}+
\begin{bmatrix}X_s\\ Y_s\\ Z_s\end{bmatrix}(6)
$$
根据公式(5,6)可得图像坐标系像世界坐标的转换的公式,此公式中的矩阵P就是要求的矩阵,实际上在控制点足够的情况下可以根据控制点直接求解P矩阵,在摄影测量中P矩阵是通过外参和内参得到,而在计算机视觉中通常并不强调世界坐标系下的绝对坐标,更感兴趣的是相对坐标,因此在计算的过程从A图像到世界坐标然后投影到B图像,这是一个典型的双目视觉的过程,而在这个过程中计算机视觉的的方法会首先根据同名点直接求解变换关系,实际上就是旋转和平移的关系,然后再通过矩阵分解的方式求解出变换矩阵。以计算机视觉的方式求解在求解过程中并不关心每一步矩阵的具体物理意义,而是将理论上非线性问题通过足够多的匹配点和控制点转换为线性问题,然后通过矩阵分解方式得到具有物理意义的参量。通过此种方式求解能够避免在求解过程中出现过多的将非线性问题转换为线性问题而出现的迭代求解的困难,但是要求控制点较多,且由于每一步都是严密求解,对求解的精度要求较高。