tensorflow-十二弹
条评论继上一讲中的几个概率的基本概念之后这次我们记录几个提的比较多,但是可能搞得不是那么明白的几个定义:
1.vc维:在介绍vc维之前首先要明白一个概念那就是散度(shatter),如果对于一个给定的集合$S={x_1,…,x_d}$ 如果一个假设类H能够实现集合S中所有元素的任意一种标记方
式,则称H能够分散S.假设对于两个样本点$A,B$其将其进行二类分类,则划分方式有 ${(A+1,B-1);(A+1,B+1);(A-1,B-1);(A-1,B+1)}$四种情况,则这两个样本的散度为 $2^2$ 实际上对于具有N个样本的数据集其散度为$2^N$, 对于一个二类分类器,我们可知二维中的一条直线对多可以实现对三个样本的集合打散,如图: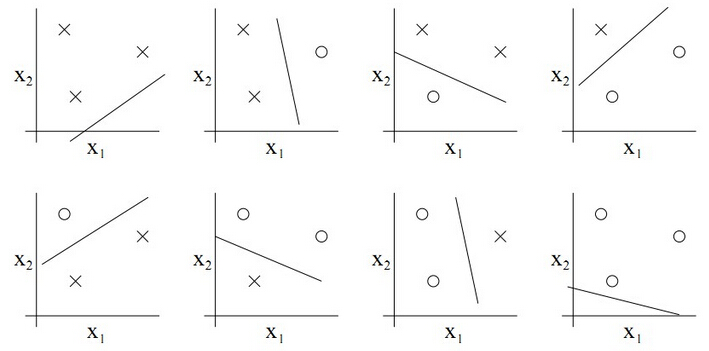
则上述8种情况包含了所有的组合.二VC维则是衡量这种分类器对于样本打散情况的量,我们说平面上直线分类器的VC维为三,当然对于三个点的情况,如果三个点处于一条直线上也有可能线性分类器无法实现全划分,但是这种情况并不影响.实际上二维平面上的找不到一条直线能够将四个点打散.但是实际上二维平面不止有线性分类器一种分类器,如下图: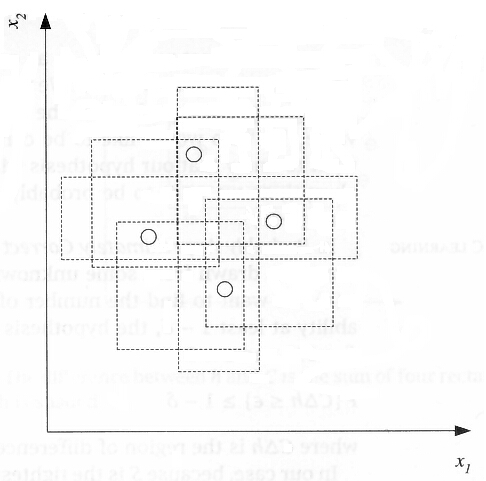
上述矩形分类器能够实现将二维空间中四个点打散,所以二维的矩形分类器的VC维是4从以上分析可以看出VC维就是能分散集合中中的最大样本数目.好了理解了VC维我们来看一个比较特殊的函数集,正弦函数集 ${asin{wx+b}}$ 我们知道正弦函数几乎可以拟合任何一种情况(傅里叶),所以对于包含任意数量的点集都能够将其打散,因此正弦函数集的VC维为无穷大.
2.非参数模型: 介绍非参数模型之前需要介绍一下参数模型,什么是参数模型,就是首先假设模型的分布的模型的已知的,在此情况下通过样本估计模型的参数,这样的模型叫做参数模型,而非参数模型假设样本分布是自由的,因此不需要对模型的参数进行估计而是通过其他的手法进行估计.
3.点估计: 点估计是有样本估计总体分布所含未知参数的真值,称为估计值,点估计的精确程度用置信区间表示,由于样本是从总体中获取,且假设每一个样本都是独立同分布,则可以用样本对总体进行估计.点估计的方法:最大似然法:最大似然法是一种使用得最广泛的点估计方法,最大似然估计就是利用已知样本的结果反推最有可能导致这样结果的参数值,假设有样本 $X={X_1,X_2,…,X_n}$ 其样本的分布密度为$L(X,\theta)$,现在样本是已知的,则将L当作 $\theta$的函数称为似然函数,则将似然函数表述为:$f(X_1,\theta),f(X_2,\theta)…f(X_n,\theta)$,其中$f(X,\theta)$ 为总体分布的密度函数或概率函数在已知样本的情况下可以分布参数进行估计;最小二乘方法,最小而乘的参数估计是保证计算的函数尽可能好的拟合观测样本从而得到拟合函数.
4.估计的无偏性:无偏估计意味这样本估计量的数学期望等于其总体分布的真值,一个估计是无偏的则说明其概率分布的期望值等于它所估计的参数,无偏性并不是说我们用任何一个特定样本得到的估计值等于d,甚或很接近0。而是说,如果我们能够从总体中抽取关于Y的无限多个样本,并且每次都计算一个估计值,那么将所有随机样本的这些估计值平均起来,我们便得到总体的均值.
5.核方法: 核方法的主要思想为,在低维空间中线性不可分的点集将其映射到高维空间中则往往变为可分的,而这个将低维空间向高维空间映射的方法我们称为核方法,实际上通过核方法将高维向量中的内积转换为低维的点的核函数计算,由此大大简化了在高维空间的计算方法,实际上核函数的构造具有很多技巧以及对于核函数是否存在也具有一套判断方法,这个设计到比较复杂的过程以后有机会在进行详细说明.
今天介绍了概率论中的一些重要的概念,这些概念对于我们理解机器学习的算法至关重要,另外机器学习的基本方法是深度学习的基础,因此我们需要将这些概念理解清楚才能够更好的学习深度学习的理论和方法.
参考资料:
VC维参考资料
非参数模型资料
点估计
核方法