混合高斯分布
条评论本来是想着做一个混合高斯分布,但是想着点云的分布应该不是混合高斯布,所以又想看看是不是应该是均匀分布,但是我仔细一想还是应该是高斯分布,因为我们现在讨论的并不是点云本身的分布特点,而是点云聚类的分布特点,实际上对于给定的类别,距离聚类中心越近属于该类别的可能性就越大,因此还是应当是高斯分布。为了更加具体的说明问题,我模拟以下两个数据集: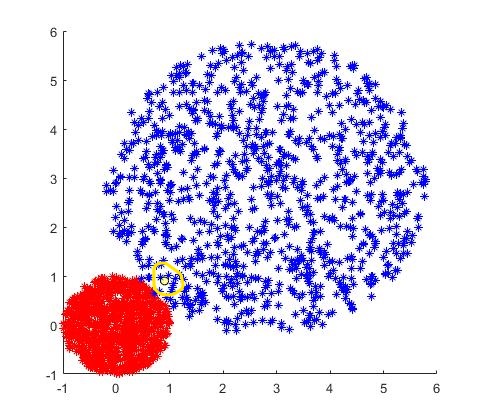
图中两个点集都是均匀分布,黄色框中为的黑色点为一个随机点,实际上我们认为我们每一个点都是随机均匀分布而且激光束发出的激光理论上也应该是均匀分布,但是实际上地物的分布有其自身的特点,且相似的地物具有聚集性(地理学第一定律)因此我们可以认为地物的分布是具有高斯分布特性的,而地物的分布实际上会影响点云在空间上的密度使其呈现出与地物分布类似的密度。因此我们有理由相信高斯分布县比喻均匀分布能够更好的对地物的分布进行拟合。
高斯分布:
$$
\begin{aligned}
&p(x)=\frac{1}{\sqrt{2}\pi}exp(-\frac{x^2}{2}) \
&p(x,y)=p(x)*p(y)=\frac{1}{\sqrt{2}\pi}exp(-\frac{x^2+y^2}{2})
\end{aligned}
$$
以上为一维和二维的标准高斯分布,实际上我们将高斯分布扩展到多维,则需要用引入向量表示,即我们用向量$v$表示一个随机向量则多变量的高斯分布可以表示为$p(v)=\frac{1}{\sqrt{2}\pi}exp(-\frac{v^Tv}{2})$,实际上方差的平方要变成协方差,但是由于是标准的正态分布,因此直接$v^Tv$计算就可以了,针对一般情况需要进行一个变换了,由于均值不为0方差存在差异,则我们假设一个线性变换,通过这个线性变换能够将变量变换到标准正态分布上,这个线性变换为$x=A(x-\mu)$,则标准的正态分布可以表示为:
$$
p(v) = \frac{|A|}{\sqrt{2}\pi}exp[-\frac{1}{2}(x-\mu)\Sigma^{-1}(x-\mu)]
$$
在上式中$\Sigma$为协方差矩阵,则上式表示的为均值为$\mu$协方差矩阵为$A^TA^-1$的$n$维正态分布。则我们模拟一个二维高斯正态分布的图为: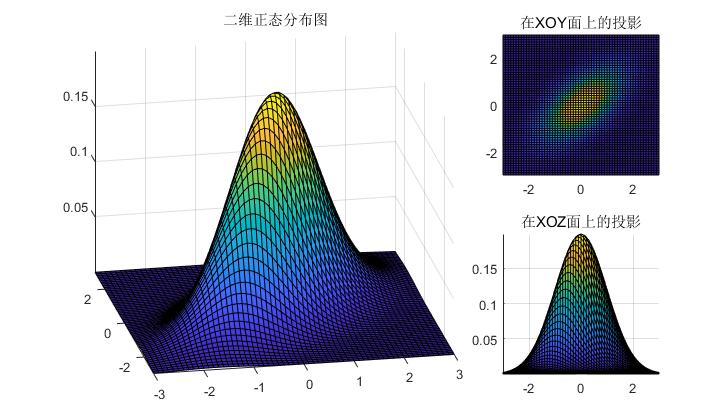
实际上高斯分布是一种常用而且简单的分布,且一般情况下地物聚类的分布特征都符合高斯分布,因此将高斯分布用来对地物进行分类是一个合理的做法。
高斯混合分布:
实际上单高斯分布相对来说比较简单,但是自然地物很少存在单高斯分布的情况,由于地物的复杂性,自然地物呈现的是聚合而且混杂的趋势,因此使用单一的高斯分布对地物分布进行拟合可能存在较大误差,此时需要考虑多高斯分布的情况:
$$
p(x)=\sum_{k=1}^{K}\pi_{k}\mathcal{N}(x|\mu_{k},\Sigma_K)
$$
其中$\mathcal{N}(x|\mu_{k})$表示为均值为$\mu_k$协方差矩阵为$\Sigma_K$的高斯分布,实际上高斯混合分布可以看作是$K$个高斯分布的求和。
从图上看,高斯混合分布如下图所示: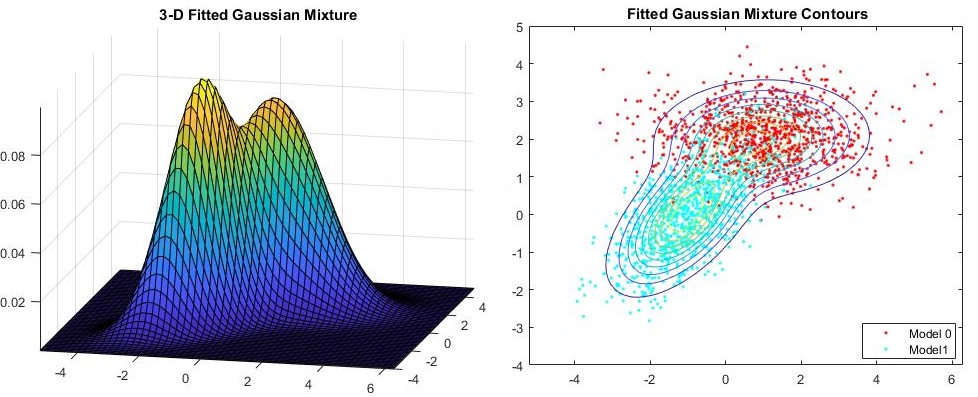
上图是两个高斯分布的模型,从上图可以看出,如果采用一个高斯函数进行拟合会存在较大的误差,拟合效果也不好,至少需要两个高斯函数进行拟合才能够达到比较好的效果。因此我们选择了一个高斯函数进行拟合时可能会存在较大的误差,由此我们也引出了下一个需要讨论的话题,理论上无限个高斯函数可以拟合任意分布,因此只要在$K$足够大的情况下可以对任意函数进行无限精确的拟合,但是这并不是我们想要的结果,这个就是我们下面需要讨论的问题,那就是高斯混合分布的求解问题。
高斯混合分布求解:
初级求解方式:
在此情况下,我们假设高斯模型的数量是已知的,那么实际上需要求解的参数就是每一个高斯模型的参数$\mu$和$\Sigma$,实际上我们需要求取的是分布的参数,那么如何求取分布参数呢,一般来说就是使得所有样本都分到最大概率的那一类中,采用的方法一般是最大似然方法,公式表示为:
$$
f=\prod_{i=1}^N p(x_i)
$$
实际上由于概率都小于1在连乘过程中容易出现精度不足的现象,因此通过取对数将连乘转换为累加进行处理。则将高斯混合分布的公式代入上式并去对数则参数求解问题转换为:
$$
max\Sigma_{i=1}^{N}log(\Sigma_{k=1}^{K}\pi_k\mathcal{N}(x_i|\mu_k,\sigma_k))
$$
对于求极值问题一般都是求导然后导数等于0进行求解,但是上式太负载,求导过于复杂因此不建议采用求导的方式求极值,一般来说是采用EM方法进行求解。
实际上对于上式的EM求解这里有一个训练的过程,一般来说给的训练数据都是$(x,label)$即数据与其所属类别,对于样本$x$它属于某一个类别$k$的概率为:
$$
\omega_i(k)=\frac{\pi_k\mathcal{N}(x|\mu_k,\sigma_k)}{\Sigma_{j=1}^{K}\sigma_j\mathcal{N}(x|\mu_j,\sigma_j)}
$$
在这里是假设所有类别的均值和协方差矩阵都是已知的,判断样本属于类别$k$的概率。因此我们是需要给出一个初始值的。由给定的初始值就可以计算出属于每一类的概率。然后对于每一类实际是要计算其期望和方差,因此已知每一个样本属于某一类后每一类的期望和方差的计算方法为:
$$
\begin{aligned}
& \mu_k=\frac{1}{N}\Sigma_{i=1}^{N}\omega_i(k)x_i \
& \sigma_k=\frac{1}{N}\Sigma_{i=1}^{N}\omega_i(k)(x_i-\mu_k)(x_i-\mu_k)^T \
&N_k=\Sigma_{i=1}^{N}\omega_i(k)
\end{aligned}
$$
分析上面的公式我们可以根据样本对每一类的均值以及方差进行重新估计,得到新的均值和方差,并以此迭代最终达到收敛。最简单的实现方式为K-Means方式,通过迭代实现聚类。
类别数目未知的情况:
实际上初级求解方式是在类别数目已知的情况下做估计,对于很多问题,特别是高斯混合分布的问题,我们通常都不知道类别数目,在此情况下求解就与简单的求解方式有着区别,因为在进行参数估计的时候还需要对类别数目有一个估计,实际上给定的类别数目越多估计肯定越准确,但是如果给定类别数目过多可能出现过拟合的现象,所以实际上我们需要对类别数目有一个约束,通常情况下有三种约束方式:$L_0,L_1,L_2$约束,解释一下,0范约束表示类别前系数$\pi_i$不为0的情况尽量多,1范约束表示类别前系数$\pi_i$的1范值尽量小,2范约束表示类别前系数$\pi_i$的2范值尽量小;
从误差的角度来说,则我们将混合高斯分布看做是对真值的拟合,则误差描述为:
$$
E(x)=f(x)+r
$$
其中$f(x)$为拟合误差,$r$为约束项,实际上我们需要使得误差最小将高斯分布代入到以上的计算过程中;则有
$$
\begin{aligned}
E(x)&=p_t(x)-p(x)+r\
&=p_t(x)-\sum_{k=1}^{K}\pi_{k}\mathcal{N}(x|\mu_{k},\Sigma_K)
\end{aligned}+\alpha\sum_{i}^K|\pi_i|
$$
上式加上了$L1$约束,则在求解过程中高斯分布的数目都是需要求解的,同样采用E-M方法进行求解,但是在求解过程中还需要对K值进行调整使其达到最佳值,实际上$\alpha$是对稀疏度的约束,在求解过程中能够体现出来,值越大则越稀疏,越小则稀疏度越低。