tensorflow-十五弹

介绍了很多关于神经网络的理论的东西，当然理论的介绍还差得远，但是再介绍理论上的东西未免显得太无聊了，所以我们中间穿插一些关于tensorflow的小技巧的介绍以及相关算法的简单说明：

• 自定义损失函数：在神经网络的学习过程中我们使用损失函数去判别学习好坏，实际上损失函数的定义有很多种，tensorflow中也内置了很多种类的损失函数，一般来说这些损失函数已经能够训练出比较好的效果了，但是对于实际问题我们常常会有着不同的要求，在此情况下所需的损失函数也会有所差异，在tensorflow中可以使用自定义的损失函数来进行约束，使得求解结果满足要求．示例代码如下：

  import tensorflow as tf
  from numpy.random import RandomState
  
  #y=wx
  batch_size = 8
  x = tf.placeholder(tf.float32,shape=(None,2),name='x-input')
  y_= tf.placeholder(tf.float32,shape=(None,1),name='y-input')
  w1= tf.Variable(tf.random_normal([2,1],stddev=1,seed=1))
  y = tf.matmul(x,w1);
  
  #loss
  """
  loss_less = 10
  loss_more = 1
  loss = tf.reduce_sum(tf.where(tf.greater(y, y_), (y - y_) * loss_more, (y_ - y) * loss_less))
  """
  """
  loss_less = 1
  loss_more = 10
  loss = tf.reduce_sum(tf.where(tf.greater(y, y_), (y - y_) * loss_more, (y_ - y) * loss_less))
  """
  loss = tf.losses.mean_squared_error(y,y_)
  
  
  ##
  train_step = tf.train.AdamOptimizer(0.001).minimize(loss)
  
  #data
  rdm = RandomState(1)
  X = rdm.rand(128,2)
  Y = [[x1+x2+(rdm.rand()/10.0-0.05)] for (x1,x2) in X]
  
  #train
  with tf.Session() as sess:
      init_op = tf.global_variables_initializer()
      sess.run(init_op)
  
      STEPS = 5000
      for i in range(STEPS):
          start = (i*batch_size)%128
          end   = (i*batch_size)%128+batch_size
          sess.run(train_step,feed_dict={x:X[start:end],y_:Y[start:end]})
          if(i%1000==0):
              print('After %d train step(s) ,w1 is: '%(i))
              print sess.run(w1), '\n'
      print 'finnal w1 is: \n',sess.run(w1)

以上代码很简单，具体过程我们就不进行详细分析，直接看损失函数定义的位置（被多行注释的位置）从损失函数定义我们可以看到定义了三种损失函数，第一种为预测值小于观测值时误差具有较大的权重，此时拟合结果偏向于观测值较大的方向，第二种为预测值大于观测值时误差具有较大的权重，此时结果偏向于观测值较小的方向，最后是均方差．从以上的误差定义可以看出我们可以使用自定义的误差函数对误差权重进行调整使得结果朝着我们预期的方向发展．

• 学习率的设置：实际上在学习过程中学习率是一个很重要的量，学习率设置得越小则每一步学习的步长越小，学习结果越精确，但是计算效率也更低，而学习率设置得值比较大，则学习效率较高但是学习结果越粗糙，因此设置合适的学习率对求解有着重要的影响，下面我们看看在tensorflow中如何对学习率进行设置：

import tensorflow as tf

'''
TRAIN_STEPs=10
LEARN_RATE = 1

x = tf.Variable(tf.constant(5, dtype=tf.float32), name="x")
y = tf.square(x)

train_op = tf.train.GradientDescentOptimizer(LEARN_RATE).minimize(y)

with tf.Session() as sess:
    sess.run(tf.global_variables_initializer())
    for i in range(TRAIN_STEPs):
        sess.run(train_op)
        x_value = sess.run(x)
        print "After %s iteration(s): x%s is %f."% (i+1, i+1, x_value)
'''
#'''
TRAINING_STEPS = 100
global_step = tf.Variable(0)
LEARNING_RATE = tf.train.exponential_decay(0.1, global_step, 1, 0.96, staircase=True)

x = tf.Variable(tf.constant(5, dtype=tf.float32), name="x")
y = tf.square(x)
train_op = tf.train.GradientDescentOptimizer(LEARNING_RATE).minimize(y, global_step=global_step)

with tf.Session() as sess:
    sess.run(tf.global_variables_initializer())
    for i in range(TRAINING_STEPS):
        sess.run(train_op)
        if i % 10 == 0:
            LEARNING_RATE_value = sess.run(LEARNING_RATE)
            x_value = sess.run(x)
            print "After %s iteration(s): x%s is %f, learning rate is %f."% (i+1, i+1, x_value, LEARNING_RATE_value)
#'''

上述代码有两种学习率设置的方式，第一种为固定一个学习率，第二种为随着迭代数的增加学习率也在随着增加，设置第一种学习方式比较简单，第二种学习方式在梯度下降算法中使用得很多，随着迭代次数的增加，计算结果也越接近真实值，此时需要降低学习率以便于能够进行更加精确的学习，而且随着学习结果越接近真值就需要更加精确的设置学习率以避免计算中出现震荡的现象．

• 正则化，这个问题想必搞学习算法的人都会有遇到，简单的来说求解求解 $argmin{||y_i-f(x;w)||^2+\lambda\Omega(w)}$的问题，其中 $||y_i-f(x;w)||^2$为损失函数，当然损失函数的定义有很多种，而 $\lambda\Omega(w)$ 为正则化项，为什么要进行正则化，这是由于在计算过程中为了使得计算结果符合奥卡姆剃刀法则,使得采用最简单的形式表示$y$与$x$之间的关系，因此采用正则项进行约束，常用的正则项包括$L0,L1,L2$ 其中$L0$ 又称为稀疏约束，说明约束项为使得参数中非０项最少．在tensorflow中可以很方便的定义正则项：

import tensorflow as tf
import matplotlib.pyplot as plt
import numpy as np

data = []
label = []
np.random.seed(0)

for i in range(150):
    x1 = np.random.uniform(-1,1)
    x2 = np.random.uniform(0,2)
    if x1**2 + x2**2 <= 1:
        data.append([np.random.normal(x1, 0.1),np.random.normal(x2,0.1)])
        label.append(0)
    else:
        data.append([np.random.normal(x1, 0.1), np.random.normal(x2, 0.1)])
        label.append(1)

data = np.hstack(data).reshape(-1,2)
label = np.hstack(label).reshape(-1, 1)
#plt.scatter(data[:,0], data[:,1], c=label,
#           cmap="RdBu", vmin=-.2, vmax=1.2, edgecolor="white")
#plt.show()
def get_weight(shape, lambda1):
    var = tf.Variable(tf.random_normal(shape), dtype=tf.float32)
    tf.add_to_collection('losses', tf.contrib.layers.l2_regularizer(lambda1)(var))
    return var

x = tf.placeholder(tf.float32, shape=(None, 2))
y_ = tf.placeholder(tf.float32, shape=(None, 1))
sample_size = len(data)


layer_dimension = [2,10,5,3,1]
n_layers = len(layer_dimension)

cur_layer = x
in_dimension = layer_dimension[0]

# full connected net
for i in range(1, n_layers):
    out_dimension = layer_dimension[i]
    weight = get_weight([in_dimension, out_dimension], 0.003)
    bias = tf.Variable(tf.constant(0.1, shape=[out_dimension]))
    cur_layer = tf.nn.elu(tf.matmul(cur_layer, weight) + bias)
    in_dimension = layer_dimension[i]

y= cur_layer

# def loss func
mse_loss = tf.reduce_sum(tf.pow(y_ - y, 2)) / sample_size
tf.add_to_collection('losses', mse_loss)
loss = tf.add_n(tf.get_collection('losses'))

#train
'''
train_op = tf.train.AdamOptimizer(0.001).minimize(mse_loss)
TRAINING_STEPS = 40000

with tf.Session() as sess:
    tf.global_variables_initializer().run()
    for i in range(TRAINING_STEPS):
        sess.run(train_op, feed_dict={x: data, y_: label})
        if i % 2000 == 0:
            print("After %d steps, mse_loss: %f" % (i,sess.run(mse_loss, feed_dict={x: data, y_: label})))

    # draw
    xx, yy = np.mgrid[-1.2:1.2:.01, -0.2:2.2:.01]
    grid = np.c_[xx.ravel(), yy.ravel()]
    probs = sess.run(y, feed_dict={x:grid})
    probs = probs.reshape(xx.shape)

plt.scatter(data[:,0], data[:,1], c=label,
           cmap="RdBu", vmin=-.2, vmax=1.2, edgecolor="white")
plt.contour(xx, yy, probs, levels=[.5], cmap="Greys", vmin=0, vmax=.1)
plt.show()
'''

# train
train_op = tf.train.AdamOptimizer(0.001).minimize(loss)
TRAINING_STEPS = 40000

with tf.Session() as sess:
    tf.global_variables_initializer().run()
    for i in range(TRAINING_STEPS):
        sess.run(train_op, feed_dict={x: data, y_: label})
        if i % 2000 == 0:
            print("After %d steps, loss: %f" % (i, sess.run(loss, feed_dict={x: data, y_: label})))

    # draw
    xx, yy = np.mgrid[-1:1:.01, 0:2:.01]
    grid = np.c_[xx.ravel(), yy.ravel()]
    probs = sess.run(y, feed_dict={x:grid})
    probs = probs.reshape(xx.shape)

plt.scatter(data[:,0], data[:,1], c=label,
           cmap="RdBu", vmin=-.2, vmax=1.2, edgecolor="white")
plt.contour(xx, yy, probs, levels=[.5], cmap="Greys", vmin=0, vmax=.1)
plt.show()

这一段代码比起上两段代码就略显复杂，因此为了更好的说明正则项带来的效果通过matplotlib库进行了图形的绘制，实际上我们可以忽略图形绘制的过程直接看正则项的设置过程，

def get_weight(shape, lambda1):
    var = tf.Variable(tf.random_normal(shape), dtype=tf.float32)
    tf.add_to_collection('losses', tf.contrib.layers.l2_regularizer(lambda1)(var))
    return var

我们看到在权重的设计过程中我们通过tf.contrib.layers.l2_regularizer(lambda1)(var)函数设置了一个$L2$正则项，通过正则项的约束可以进行求解，为了直观的看到约束结果做图如下：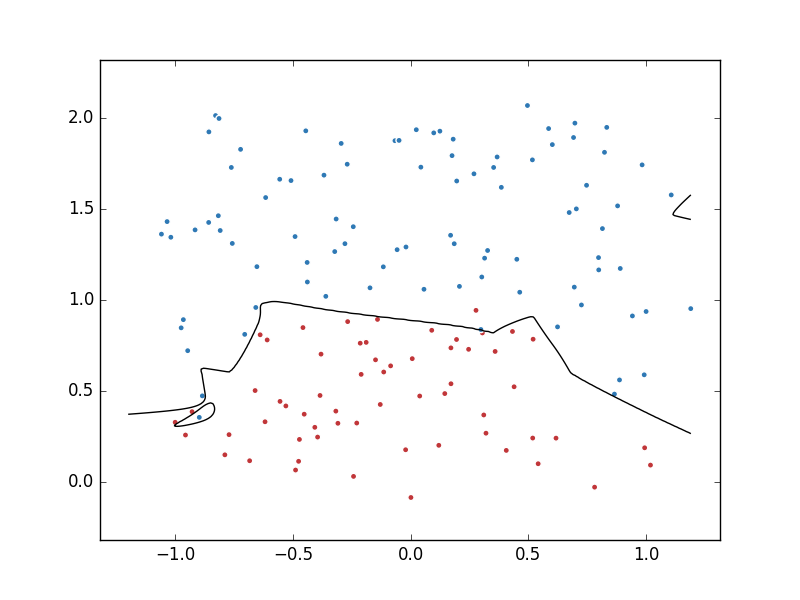

上图是无正则化项的求解结果，从求解结果可以看出在无正则化的情况下出现了比较明显的过拟合现象，过拟合现象的存在极大的降低了模型的泛化性能，使得求解结果不理想．　　

上图是添加了正则项的求解结果，从求解结果上比较，添加了正则项后虽然样本的拟合误差有所增加但是模型更加简单，增加了模型的泛化性，因此添加正则项后的模型更具有普适性，具有更好的效果．
以上所有代码都可以再Github中找到，传送门