tensorflow-十四弹
条评论在上一讲中我们已经结束了传统学习算法的学习,马上要转入深度学习,那么在这里就不得不进行一些铺垫的工作,为什么我们要提深度学习,传统的学习方法究竟在哪些地方不如深度学习,是否有可能这些缺点会被克服以及深度学习的所面对的问题.
总的来说,促使机器学习发展的部分原因在于传统学习算法对于高维,复杂函数的泛化性较差,在高维空间中的复杂函数的学习传统的学习方法往往面临着巨大的计算代价,而促进机器学习发展的主要有两点,1.维度灾难;2.流型学习.下面分别就这两个问题进行进一步的描述:
维度灾难
这个问题是最好理解的问题,当数据的维数很高的时候传统的机器学习算法会变得相当困难,甚至面临无法求解的情况,另外随着变量维数的增加或函数复杂性的增加,求解的规模呈现指数增长模式,在机器学习中此问题尤为突出,由维数灾难带来的一个挑战是统计挑战,随着求解规模的增加,样本数在不增加的情况下变量数增加了,由此产生统计上的不确定性,这个问题可以通过图进行简单描述: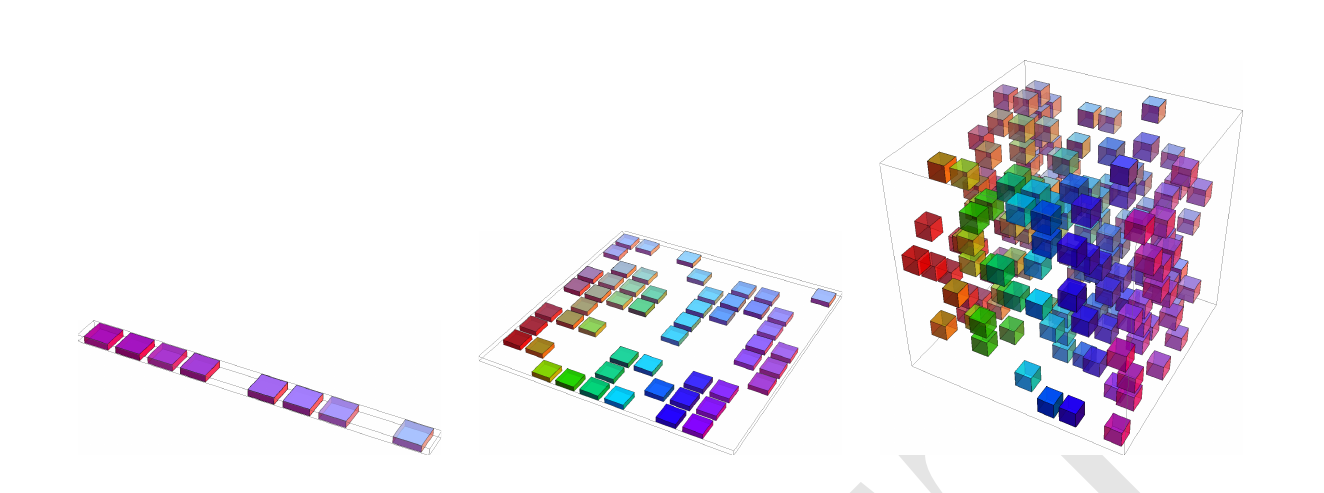
从左到右维数增加了,为了对空间具有统计性,我们所需要的样本数量也大大增加了,而采用同样数量的样本无法充满增加维数的空间,或者说对增加维数的空间不具有统计特征.而传统的学习方法通常都有两个假设,平滑先验性和局部不变性,实际上意思就是在空间中处处可导,不会产生突变,这样在拟合的过车给你中可以通过真实值周围的值对真值进行估计,而随着维度的增加,在某一个维度上满足这两个特征的变量在其他维度上可能不满足.
流型学习
流型简单的来说就是指连在一起的区域,实际上对于我们所处的样本空间,我们认为空间中大部分的数据都是无效区域,有意义的区域只包含在包含少量数据点构成的子集中,而学习函数的输出中有意义的变化都沿着流型方向或仅仅发生在切换到另一个流型的过程中,实际上也满足这个要求,对于影像像素,我们对没一个像素值都随机取值,实际上构成影像的概率几乎为0,而我们获取的影像可以认为是影像空间的流型.流型学习模型允许我们通过少量的学习样本在空间中找到有意义的流型.