tensorflow-第三弹
条评论好不容易可以发第三弹了,在这一回的学习和编码过程中遇到了很多的坑,当然咯,要做机器学习特别是用一门自己并不是很熟悉的语言去做,总归是有一些坑的,不过好在这些坑在这两天都被我填上了,所以现在也可以记录一下。在上一回的学习过程中我们通过tensorflow的简单逻辑回归的拟合说明了tensorflow的图的构造以及启动的过程,这一次准备做一些更加深入的学习,采用BPNN对MNIST手写数字库进行分析和识别。首先介绍一些MNIST库,如果做过机器学习和手写数组识别的人入门必备的一个数据,数据包括6w个28×28大小的手写数字图标和它们的label,以及1w个测试样本。数据全部以二进制形式存储,所以读取很方便,另外在tensorflow的教程中已经存在了MNIST数据读取的功能,极大的简化了我们的处理,让我们专注于神经网络结构的设计。
下面我们分析一下神经网络结构的设计,我们做的是最简单的BP神经网络,也就是三层前馈神经网络,其结构如图: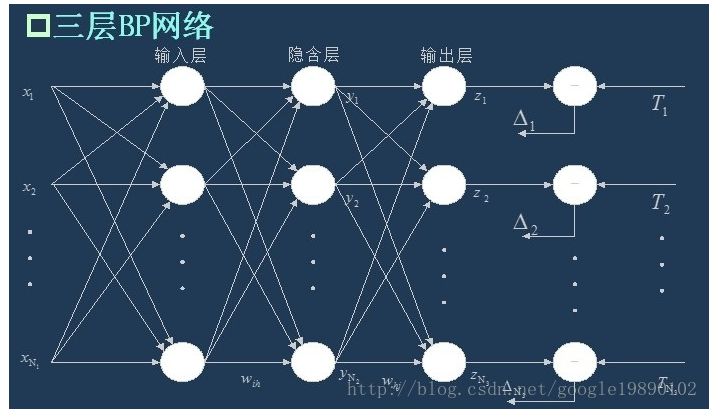
上图是一个比较好的三层BP神经网络的示意图,从图上可以看到假设样本有 $x={x_1,x_2….x_N}$ N个变量,则输入为一个N维的向量,关于这一点在做多波段图像的同学们可能需要注意一下,到底什么是样本什么是变量搞清楚。这N个变量作为输入层,然后输入层经过如下运算得到隐含层:
$h=W\cdot x+b$ (1)
隐含层的神经元的数目是给定的,为什么要给定隐含层的神经元数目,这个确定了隐含层的复杂度,理论上来说隐含层的神经元数目越多其拟合效果应该更好,但是隐含层神经元数目太多会导致两个问题(1)参数数目成指数增长,需要更多的训练样本才能进行充分学习;(2)出现对结果变化影像很小的无效参数,这些参数对结果的贡献很小,甚至可以忽略不计,除了增加计算复杂度再没有别的作用,因此应该去掉这些参数。所以合理的设置隐含层个数的问题也是神经网络调参过程的一个重要问题。
在(1)式中我们得到了隐含层的输入,实际上对于隐含层,其并不是输入等于输出,而是有一个响应函数,将输入从 $[+\infty,-\infty]$ 转换到[-1,1]这种转换有很多种,一般来说满足条件的转换有,sigmoid转换,tanh转换,relu转换等,采用这些转换是因为这些转换有一些特点,1.单调,2.在区间内处处可导;在选取这些函数后我们得到隐含层的输出,然后对应隐含层到输出层:
$o=W_2 \cdot h+b$ (2)
然后输出层与label结果比较,通过比较可得误差,然后通过误差调整误差函数 $\Delta$ 然后通过调整得到输出层的 $W_2$ 和 $b2$ 然后得到计算的 $h$和实际 $h$ 之间的差距然后对数据进行调整 $w1$ 和$b1$ 。至于如何调整,一般来说采用的是梯度下降法进行调整,至于为什么能够进行最优的求解,具体的算法分析可以参考其他文档,在这里并不做详细的分析,我的其他博客上有具体的分析。好了,分析完BPNN的原理之后我们看看其实现的代码:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49import tensorflow as tf
import numpy as np;
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("mnist/MNIST_data/", one_hot=True)
with tf.name_scope('input'):
x = tf.placeholder(tf.float32, [None, 784],name = 'x-input')
y = tf.placeholder("float", [None, 10],name='y-input')
x_image = tf.reshape(x,[-1,28,28,1],name='img')
tf.summary.image('image',x_image,20)
w1 = tf.Variable(tf.truncated_normal(shape=[784,50],stddev=0.1))
init1 = tf.constant(0.1, shape=[50])
b1 = tf.Variable(tf.zeros([50]),
name='biases1')
w2 = tf.Variable(tf.truncated_normal(shape=[50,10],stddev=0.1))
init2 = tf.constant(0.1, shape=[10])
b2 = tf.Variable(tf.zeros([10]),
name='biases2')
hidden1 = tf.nn.relu(tf.matmul(x,w1)+b1)
y_ = tf.nn.relu(tf.matmul(hidden1,w2)+b2)
with tf.name_scope('loss'):
loss = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(labels=y, logits=y_))
tf.summary.scalar('loss',loss)
with tf.name_scope('accuracy'):
with tf.name_scope('correct-predict'):
correct_predict = tf.equal(tf.argmax(y, 1), tf.argmax(y_, 1))
with tf.name_scope('accuracy'):
accuracy = tf.reduce_mean(tf.cast(correct_predict, "float"))
merged = tf.summary.merge_all()
step = tf.train.GradientDescentOptimizer(0.1).minimize(loss)
with tf.Session() as sess:
writer = tf.summary.FileWriter('tensorflow-start_Log', sess.graph)
sess.run(tf.global_variables_initializer())
for i in range(100000):
batch_xs, batch_ys = mnist.train.next_batch(100)
summary,_=sess.run([merged,step], feed_dict={x: batch_xs, y: batch_ys})
if i%1000 == 0:
train_acc = accuracy.eval(feed_dict={x: batch_xs, y: batch_ys})
print('step',i,'training accuracy',train_acc)
writer.add_summary(summary, i)
代码没有什么好分析的,主要就是构建输入,构建权重函数和偏置函数,然后构建损失函数和梯度下降算法,最后通过run函数运行整个图,代码就不进行具体分析了,我们需要进行更加具体分析的是其中的坑。在一开始的时候总是发现训练精度没法提高,总是很奇怪不知道为啥,后来一步步的排查发现了问题,问题主要在于w和b,由于w和b是需要调整的变量,因此需要将他们设置为variable,这一个问题困扰了我几天,终于发现了这个问题,在调整这个问题之后所有的问题都迎刃而解了,另外一个就是tensorboard的问题,总是没有办法正确的运行,也困扰了很久,为什么会有这样的问题,主要原因在于路径的错误,另外再设置参数的过程中不能加上引号,这样才能运行tensorboard,好了,下面看看我们简单的BPNN构建的图:
好了,我们分析上面的图,有几个大节点我们需要注意,首先是Input的节点,Imput节点包括x和y,然后实现matmul和add函数,并通过relu函数进行映射,然后得到hidden层,然后再通过w和b和relu得到输出,通过比较loss函数通过梯度下降法对所有的w和b进行调整,整个过程再graph中一目了然。